Trading

Introduction

The Masters course in Advanced Computer Science at the University of Exeter required a dissertation project. I chose to research and develop a quantitative trading algorithm, more specifically a statistical arbitrage strategy that sought to identify and capitalise on market inefficiencies shown within the top 500 United States equities.

Statistical Arbitrage

The premise of the trading strategy was based on pairs trading, that is if you have two stocks that have some underlying economic connection the prices of those stocks will be somewhat related to each other and thereby creating a relationship between two different stocks. This relationship is sometimes able to be exploited, for instance say the demand for a service two companies provide increases, we would assume the stock price to go up for both stocks. This will likely happen but due to inefficiencies in the stock market, prices may not always be representative of the true value and one stock’s price may undeservedly rise higher than another. In this case we can predict that with a decent probability the stock prices will eventually come closer together and place a trade accordingly.

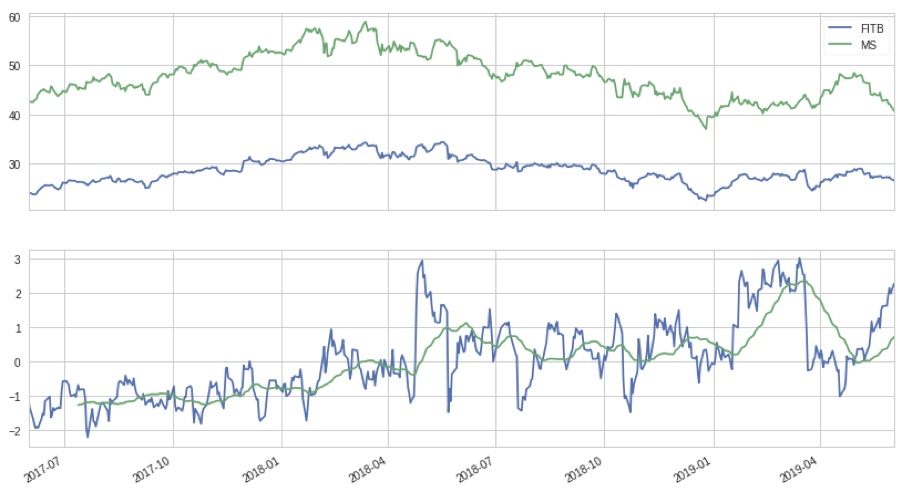
The graph below show this relationship with two real stocks Fifth Third Bank and Morgan Stanley. The top graph shows their respective stock prices and the lower graph shows the difference or spread between them. A simple version of this strategy is to use a moving average over this spread to determine our entry points. That is when we start a trade, for instance when the z-index or y value on the bottom graph crosses over 1 we make a trade - shorting one stock and going long on another. As shown by the graph the spread usually reverts from its extreme and tends towards the centre, after a sufficient change in the spread we can close the trade and realise profits.

Quantitative Research

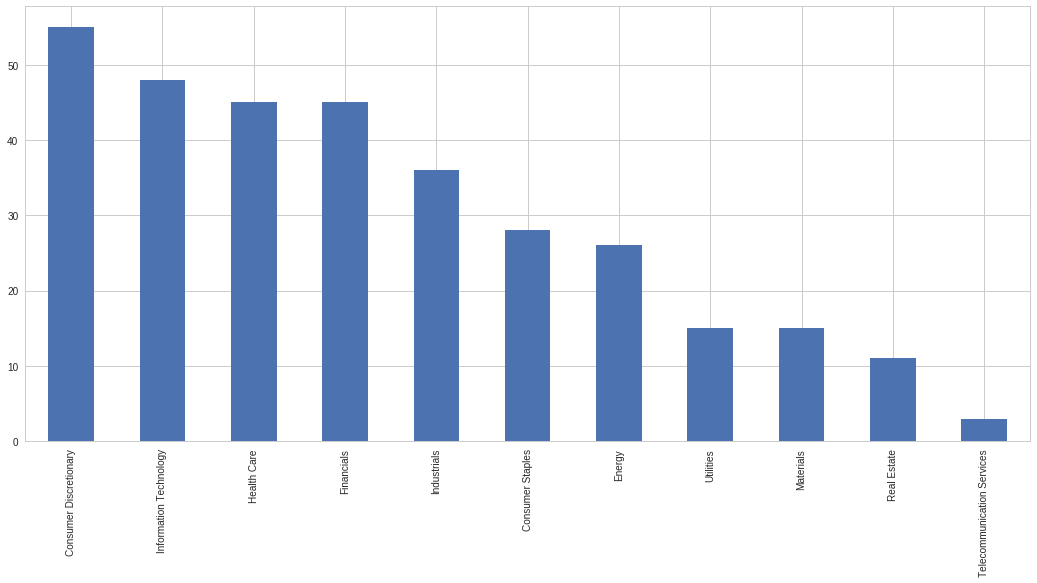
The research involved an initial exploration and cleansing stage where I manipulated the data from the Quantopian platform into something that would be easier for me to work with. The second step was to split the large collection of 500 stocks into more cohesive groups in an attempt to avoid inflation bias. I did this by retrieving industrial sector data on the equities and then dividing them accordingly. The sizes of those categories are shown below.

Cointegration is a statistical property of a collection of time series variables. It can be used in order to determine whether variables have some underlying connection. There is cointegration if, for a collection of time series variables, all with order of integration d, there exists some linear combination of that collection that is integrated of order less than d.

In the case of pairs trading we use the mean reversion property in order to capitalise on pricing inefficiencies, this means that the spread between two stocks must be stationary so we can predict its future movements and consequently the stocks themselves. To avoid inflation bias I used two methods for identifying cointegration in this project, the Engle-Granger and Johansen tests.

Results

I created two algorithms during my time on this project, the first algorithm I created was the simple program that used the moving average and the hedge ratio found from linear regression in order to decide upon the z-score. The other algorithm used a Kalman Filter to retrieve the expected true value of the stock prices (in place of the moving average) and also a Kalman filter to calculate the hedge ratio. The table below shows the results of these algorithms. The data used was using a data range from the 1st January 2019 to the 1st January 2020. This data was also used during the research to find cointegrating stocks. This was intentional as it allows a comparison of the simple and more complex methods against without the complication of whether the stocks are continuing to exhibit that relationship.

Algorithm	Alpha	Beta	Sharpe	Drawdown	Returns
Simple	0.11	0.26	0.57	-28.72%	13.71%
Complex	0.62	-0.54	1.67	-10.18%	54.87%

The comparison shows that when using data that is cointegrated the Kalman filter provides an advantage, in fact the more complex algorithm was better in all categories. It achieved great returns whilst maintaining a very low drawdown percentage, it had a better Alpha, Beta and Sharpe ratio. However it should be stated that the simple algorithm has still outperformed the market but with a large drawdown it would be quite risky using this algorithm. Overall it appears as if the Kalman filter has undoubtedly outperformed the simple algorithm in this case.

The next experiment was to therefore test the algorithms using unseen data. The table below shows the output of those results. The following data was using a date range from the 1st January 2020 to the 1st August 2020. It is important to note that during this period the global market crash occurred to complications of the COVID-19 pandemic.

Stock - x	Stock - y	Alpha	Beta	Sharpe	Returns	Drawdown
COF	CFG	-0.23	-0.57	-0.38	-28.35%	-53.87%
FITB	MS	0.30	0.41	1.21	19.42%	-17.92%
ICE	PGR	0.36	0.04	2.33	22.56%	-3.77%
ABC	DVA	-0.17	-0.43	-0.52	-15.93%	-22.72%
Portfolio		0.24	-0.47	0.23	-7.2%	-50.64%

These final results using the complex algorithm showed that whilst two of the stocks made decent returns there was also two that did not, after looking at the graph comparing the these failing stocks it was clear that the cointegrating relationship has either broken down or had never existed, one potential cause of this could have been the pandemic, which caused large volatility in the markets and meant my parameters for initiating trades were not suited for the market conditions.